Homework 3

Jio Gim, Creative IT Engineering, POSTECH
Student ID: 20160087, Povis ID: iknowme

🤔 Tip: This page uses KaTeX feature of Gitlab. If you are watching this document in Github, look this prerendered README.

Sudoku Board

How I used CNF to solve E/O Sudoku game

Value Mapping

In my solver (named SUDOKUS), $`x_{(i,j,k)}`$ which means whether if $`i`$ th row $`j`$ th column has value $`k`$ is mapped to $`ijk`$. For example, when $`777`$ is true, the cell of $`7`$ th row $`7`$ th column should have a value of $`7`$.

CNF Making

Below items are conjuncted.

• All possibilities for an empty cell
  For all empty cells, add condition of its all possibilities. For instance, in the cell of $`7`$ th row $`7`$ th column on right figure, the number $`1`$, $`3`$, $`5`$, $`7`$, $`9`$ cannot be in there. So in this case, the condition $`(x_{(7,7,2)}\lor x_{(7,7,4)}\lor x_{(7,7,6)} \lor x_{(7,7,8)})\land \lnot x_{(7,7,1)} \land \lnot x_{(7,7,3)} \land \lnot x_{(7,7,5)} \land \lnot x_{(7,7,7)} \land \lnot x_{(7,7,9)}`$ will be included to the CNF sentence. In this phase, Even/Odd Sudoku rules are also applied.

• Basic Sudoku rules
  There're three major rule: $`1`$ to $`9`$ in each sub-grid, in each column, and in each row. This can be expressed in CNF as below.

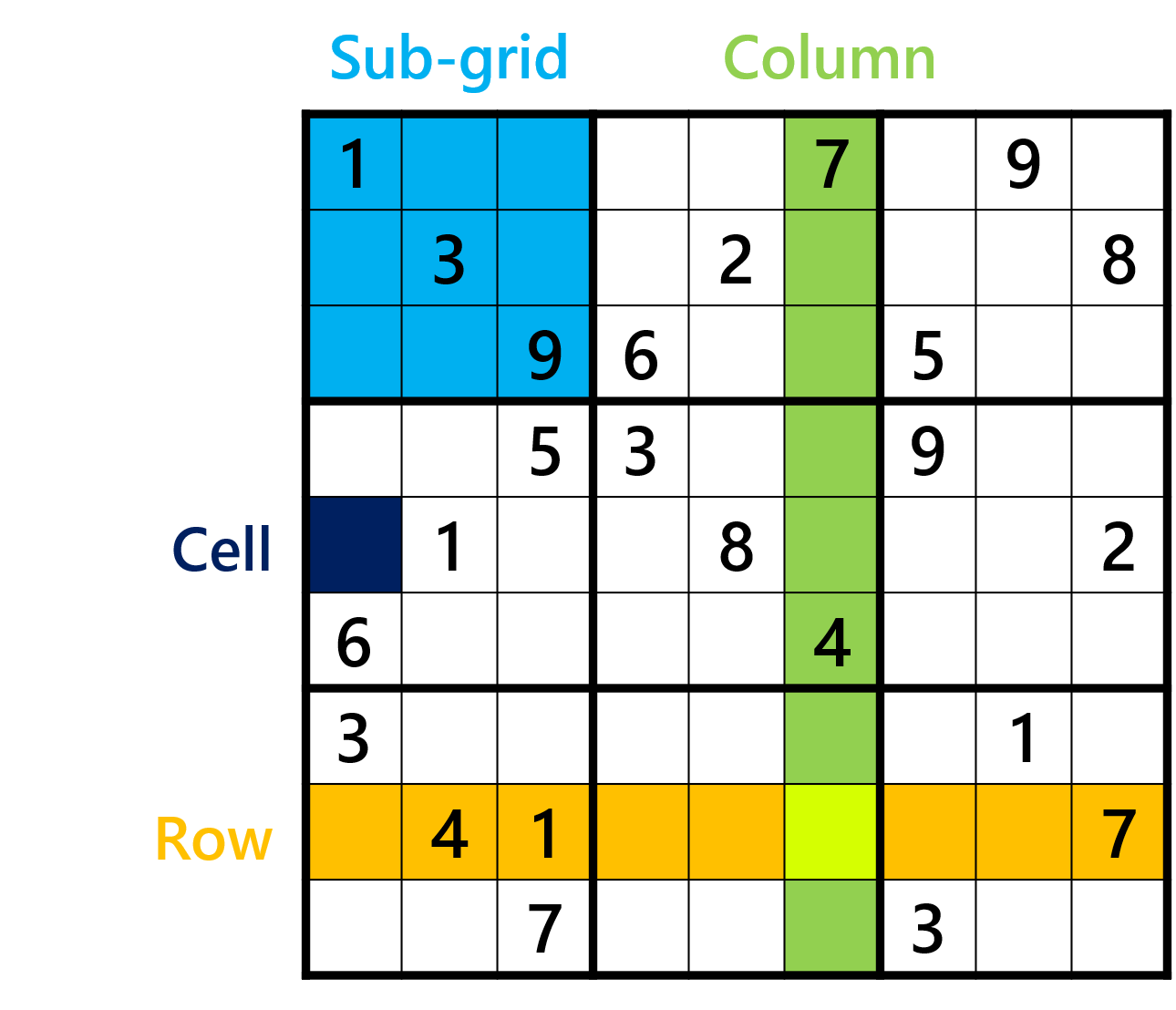
  • Sub-grid level
    $`(x_{(1,1,1)} \lor x_{(1,2,1)} \lor x_{(1,3,1)} \lor x_{(2,1,1)} \lor x_{(2,2,1)} \lor x_{(2,3,1)} \lor x_{(3,1,1)} \lor x_{(3,2,1)} \lor x_{(3,3,1)})`$
    $`\land (x_{(1,1,2)} \lor x_{(1,2,2)} \lor x_{(1,3,2)} \lor x_{(2,1,2)} \lor x_{(2,2,2)} \lor x_{(2,3,2)} \lor x_{(3,1,2)} \lor x_{(3,2,2)} \lor x_{(3,3,2)})`$
    $`\cdots`$
    $`\land (x_{(1,1,9)} \lor x_{(1,2,9)} \lor x_{(1,3,9)} \lor x_{(2,1,9)} \lor x_{(2,2,9)} \lor x_{(2,3,9)} \lor x_{(3,1,9)} \lor x_{(3,2,9)} \lor x_{(3,3,9)})`$

  • Row level
    $`(x_{(1,1,1)} \lor x_{(1,2,1)} \lor x_{(1,3,1)} \lor x_{(1,4,1)} \lor x_{(1,5,1)} \lor x_{(1,6,1)} \lor x_{(1,7,1)} \lor x_{(1,8,1)} \lor x_{(1,9,1)})`$
    $`\land (x_{(1,1,2)} \lor x_{(1,2,2)} \lor x_{(1,3,2)} \lor x_{(1,4,2)} \lor x_{(1,5,2)} \lor x_{(1,6,2)} \lor x_{(1,7,2)} \lor x_{(1,8,2)} \lor x_{(1,9,2)})`$
    $`\cdots`$
    $`\land (x_{(1,1,9)} \lor x_{(1,2,9)} \lor x_{(1,3,9)} \lor x_{(1,4,9)} \lor x_{(1,5,9)} \lor x_{(1,6,9)} \lor x_{(1,7,9)} \lor x_{(1,8,9)} \lor x_{(1,9,9)})`$

  • Column level
    $`(x_{(1,1,1)} \lor x_{(2,1,1)} \lor x_{(3,1,1)} \lor x_{(4,1,1)} \lor x_{(5,1,1)} \lor x_{(6,1,1)} \lor x_{(7,1,1)} \lor x_{(8,1,1)} \lor x_{(9,1,1)})`$
    $`\land (x_{(1,1,2)} \lor x_{(2,1,2)} \lor x_{(3,1,2)} \lor x_{(4,1,2)} \lor x_{(5,1,2)} \lor x_{(6,1,2)} \lor x_{(7,1,2)} \lor x_{(8,1,2)} \lor x_{(9,1,2)})`$
    $`\cdots`$
    $`\land (x_{(1,1,9)} \lor x_{(2,1,9)} \lor x_{(3,1,9)} \lor x_{(4,1,9)} \lor x_{(5,1,9)} \lor x_{(6,1,9)} \lor x_{(7,1,9)} \lor x_{(8,1,9)} \lor x_{(9,1,9)})`$

  • For all sets of disjunctions above: Make negative tuples of nonsame elements of them to make no any duplicated candidates get still alive in solutions.
    $`(x_{(1,1,1)} \lor x_{(2,1,1)} \cdots x_{(9,1,1)})`$ $`\rightarrow (\lnot x_{(1,1,1)} \lor \lnot x_{(2,1,1)}) \land (\lnot x_{(1,1,1)} \lor \lnot x_{(3,1,1)}) \land \cdots \land (\lnot x_{(8,1,1)} \lor \lnot x_{(9,1,1)})`$

References

• XOR to CNF: https://math.stackexchange.com/questions/636119/find-dnf-and-cnf-of-an-expression
• Compared Solver: https://sudokuspoiler.azurewebsites.net/OddEvenSudoku

Development Notes

• DO NOT USE Lombok → It does not supports Java 10.
• Logging in file output is now turned off to keep my score safe. It can re-turned on by uncommenting all comments in src/test/resources/logback-test.xml.